神经网络
感知机通过组合,可以变得很强大。
但是有个关键问题,即权重的设定,实在是太麻烦了。
神经网络,即是为了解决这个问题。实现自动从数据中学习到合适的权值参数
引例
神经网络一般分成三个部分:输入层,中间层(隐藏层),输出层。
若中间层只有一层,则实际有权重的只有输入和中间,故将其称为二层神经网络:输入1层+中间1层。
感知机的偏置b,实际可以理解为一个值始终为1,权值为b的输入。
如此一来,偏置也可以理解为参数问题。故要解决的只有参数了。
将偏置统一后,输出判定函数亦可改成与0进行比较。
引入h(x)来定义这个函数。则
$$y=h(b+\omega_1x_1+\omega_2x2)$$
$$
h(x)=
\begin{cases}
0(x\leq0)\
1(x>1)
\end{cases}
$$
激活函数
这个h(x)即可认为是激活函数。作用在于决定何时输出1。
这样一个神经元可以分成两部分。
第一部分计算sum,即$a=b+\omega_1x_1+\omega_2x2$
第二部分将结果传递给激活函数,这里是$y=h(sum)$
下面介绍一些激活函数
sigmoid函数
$$ h=\frac{1}{1+\exp(-x)}$$
看起来复杂,实际也仅仅是个函数,理解成输入输出即可。
与阶跃函数比较:
阶跃函数实现
即上文的h(x)
实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
def step_function(x):
if(x>0):
return 1
else:
return 0
import numpy as np
def step_function(x):
y=x>0
return y.astype(np.int)
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
x=np.array([-1.0,1.0,2.0])
print(x)
y=x>0
print(y)
print(y.dtype)
y=y.astype(np.int32)
print(y)
|
[-1. 1. 2.]
[False True True]
bool
[0 1 1]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
import numpy as np
import matplotlib.pylab as plt
def step_function(x):
return np.array(x>0,dtype=np.int32)
x=np.arange(-5.0,5.0,0.1)
y=step_function(x)
plt.plot(x,y)
plt.ylim(-0.1,1.1)
plt.show()
|
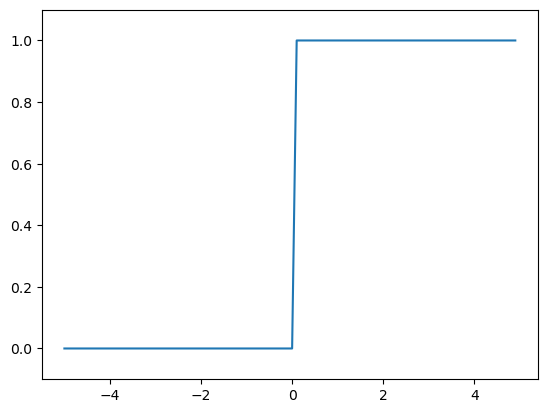
sigmoid函数实现
1
2
3
4
5
6
7
8
9
|
def sigmoid(x):
return 1/(1+np.exp(-x))
x=np.array([-1.0,1.0,2.0])
print(sigmoid(x))
|
[0.26894142 0.73105858 0.88079708]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
import numpy as np
import matplotlib.pylab as plt
def sigmoid(x):
return 1/(1+np.exp(-x))
x=np.arange(-5.0,5.0,0.1)
y=sigmoid(x)
plt.plot(x,y)
plt.ylim(-0.1,1.1)
plt.show()
|
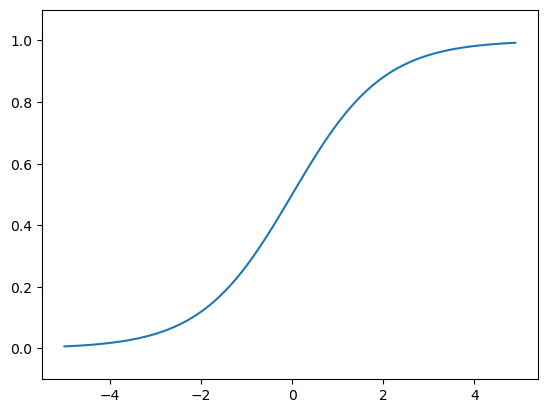
比较
- 不同:
根据图像很容易看出不同。
sigmoid函数具有光滑的性质,故其可以输出许多中间值,例如0.712,0.435…
但阶跃函数只能输出0 or 1,选择激活或者不激活。
- 相同:
两者都是在输入小时,输出接近0;输入大时,输出接近1。
两者的输出都介于0和1之间。
非线性函数
线性函数的一个很大的问题是无法发挥隐藏层优势。即设线性函数为$$ h(x)=cx$$
则三层神经网络,等于$$h(h(h(x)))$$然而这实际上就是$$h(x)=a \times x \ a=c^3$$
ReLU 函数
Rectified Linear Unit
特性:在输入大于0时,输出该值;在输入小于0时,输出0
$$h(x)=\begin{cases}
x(x>0)\
0(x\leq 0)
\end{cases}$$
1
2
3
4
5
|
def relu(x):
return np.maximum(0, x)
|
多维数组运算
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
import numpy as np
A=np.array([1,2,3,4])
print(A)
print(np.ndim(A))
print(A.shape)
print(A.shape[0])
|
[1 2 3 4]
1
(4,)
4
1
2
3
4
5
6
7
8
9
10
11
|
B=np.array([[1,2],[3,4],[5,6]])
print(B)
print(np.ndim(B))
print(B.shape)
|
[[1 2]
[3 4]
[5 6]]
2
(3, 2)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
|
print("A:2x2 B:2x2 : ")
A=np.array([[1,2],[3,4]])
print(A.shape)
B=np.array([[5,6],[7,8]])
print(B.shape)
print(np.dot(A,B))
print("\nA:2x3 B:3x2 : ")
A=np.array([[1,2,3],[4,5,6]])
print(A.shape)
B=np.array([[1,2],[5,6],[7,8]])
print(B.shape)
print(np.dot(A,B))
|
A:2x2 B:2x2 :
(2, 2)
(2, 2)
[[19 22]
[43 50]]
A:2x3 B:3x2 :
(2, 3)
(3, 2)
[[32 38]
[71 86]]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
X=np.array([1,2])
print(X.shape)
W=np.array([[1,3,5],[2,4,6]])
print(W)
print(W.shape)
Y=np.dot(X,W)
print(Y)
|
(2,)
[[1 3 5]
[2 4 6]]
(2, 3)
[ 5 11 17]
3层神经网络实现
$$w^{(1)}{12}\
w^{(1)}代表第1层权重\
w{1.}代表后一层第1个神经元\
w_{.2}代表前一层第2个神经元$$
注意,越“前”即越靠近输出层,越“后”越靠近输入层
各层传递
$$a^{(1)}1=\omega^{(1)}{11}x_1+\omega^{(1)}{12}x_2+\omega^{(1)}{13}x_3\矩阵形式:A^{(1)}=XW^{(1)}+B^{(1)}
$$
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
X=np.array([1.0,0.5])
W1=np.array([[0.1,0.3,0.5],[0.2,0.4,0.6]])
B1=np.array([0.1,0.2,0.3])
print("W1.shape : "+str(W1.shape))
print("X.shape : "+str(X.shape))
print("B1.shape : "+str(B1.shape))
A1=np.dot(X,W1)+B1
print("A1 : "+str(A1))
Z1=sigmoid(A1)
print("Z1 : "+str(Z1))
|
W1.shape : (2, 3)
X.shape : (2,)
B1.shape : (3,)
A1 : [0.3 0.7 1.1]
Z1 : [0.57444252 0.66818777 0.75026011]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
W2=np.array([[0.1,0.4],[0.2,0.5],[0.3,0.6]])
B2=np.array([0.1,0.2])
print(Z1.shape)
print(W2.shape)
print(B2.shape)
A2=np.dot(Z1,W2)+B2
Z2=sigmoid(A2)
print("A2 : "+str(A2))
print("Z2 : "+str(Z2))
|
(3,)
(3, 2)
(2,)
A2 : [0.51615984 1.21402696]
Z2 : [0.62624937 0.7710107 ]
输出层的激活函数与隐藏层有所不同
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
def identity_function(x):
return x
W3=np.array([[0.1,0.3],[0.2,0.4]])
B3=np.array([0.1,0.2])
A3=np.dot(Z2,W3)+B3
Y=identity_function(A3)
print("Y: "+str(Y))
|
Y: [0.31682708 0.69627909]
代码实现总结
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
|
def init_network():
network = {}
network['W1'] = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]])
network['b1'] = np.array([0.1, 0.2, 0.3])
network['W2'] = np.array([[0.1, 0.4], [0.2, 0.5], [0.3, 0.6]])
network['b2'] = np.array([0.1, 0.2])
network['W3'] = np.array([[0.1, 0.3], [0.2, 0.4]])
network['b3'] = np.array([0.1, 0.2])
return network
def forward(network, x):
W1, W2, W3 = network['W1'], network['W2'], network['W3']
b1, b2, b3 = network['b1'], network['b2'], network['b3']
a1 = np.dot(x, W1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1, W2) + b2
z2 = sigmoid(a2)
a3 = np.dot(z2, W3) + b3
y = identity_function(a3)
return y
network = init_network()
x = np.array([1.0, 0.5])
y = forward(network, x)
print(y)
|
[0.31682708 0.69627909]
输出层设计
一般而言,回归问题用恒等函数,分类问题用softmax函数
恒等函数和softmax函数
恒等函数不改变值,直接输出即可。
softmax函数如下
$$y_k=\frac{\exp{(a_k)}}{\sum_{i=1}^n \exp{(a_i)}}\
分子:输入信号a_k的指数函数\
分母:所有输入信号指数函数之和$$
1
2
3
4
5
6
7
|
a=np.array([0.3,2.9,4.0])
exp_a=np.exp(a)
print(exp_a)
|
[ 1.34985881 18.17414537 54.59815003]
1
2
3
4
5
|
sum_exp_a=np.sum(exp_a)
print(sum_exp_a)
|
74.1221542101633
1
2
3
4
5
|
y=exp_a/sum_exp_a
print(y)
|
[0.01821127 0.24519181 0.73659691]
1
2
3
4
5
6
7
8
9
10
11
|
def softmax(a):
exp_a=np.exp(a)
sum_exp_a=np.sum(exp_a)
y=exp_a/sum_exp_a
return y
|
softmax函数的实现,在计算机运算上有一定的缺陷。即容易溢出。
故进行如下改进
$$ y_k=\frac{\exp{a_k+C^{‘}}}{\sum_{i=1}^{n}\exp{a_i+C^{‘}}}$$
分子分母同时乘一个常数,值是不改变的。一般选取C'为输入信号的最大值
1
2
3
4
5
6
7
8
9
10
11
|
a=np.array([1010,1000,990])
print(np.exp(a)/np.sum(np.exp(a)))
c=np.max(a)
print(a-c)
print(np.exp(a-c)/np.sum(np.exp(a-c)))
|
1
2
3
4
5
6
7
8
9
10
11
12
13
| [nan nan nan]
[ 0 -10 -20]
[9.99954600e-01 4.53978686e-05 2.06106005e-09]
C:\Users\Pigeon\AppData\Local\Temp\ipykernel_15560\2797153748.py:2: RuntimeWarning: overflow encountered in exp
print(np.exp(a)/np.sum(np.exp(a)))
C:\Users\Pigeon\AppData\Local\Temp\ipykernel_15560\2797153748.py:2: RuntimeWarning: invalid value encountered in true_divide
print(np.exp(a)/np.sum(np.exp(a)))
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
def softmax(a):
c=np.max(a)
exp_a=np.exp(a-c)
sum_exp_a=np.sum(exp_a)
y=exp_a/sum_exp_a
return y
|
1
2
3
4
5
6
7
8
9
|
a=np.array([0.3,2.9,4.0])
y=softmax(a)
print(y)
print(np.sum(y))
|
[0.01821127 0.24519181 0.73659691]
1.0
softmax函数特征
由于总和是1,故可以将其理解为不同输出的概率分布
如上结果,可认为y[0]的概率为0.018,y[1]的概率为0.245,y[2]的概率为0.737
故可以解释为:因为第2个元素概率最高,所以答案是第2个类别
或者:有74%的概率是第2个类别,25%是第1个类别,1%是第0个类别
softmax函数是单调递增函数,故它不会改变元素之间的大小关系。
手写数字识别
MINISET是一个包含了数字图像的训练集。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
|
import sys, os
sys.path.append(os.pardir)
import numpy as np
from source.dataset.mnist import load_mnist
from PIL import Image
def img_show(img):
pil_img = Image.fromarray(np.uint8(img))
pil_img.show()
(x_train, t_train), (x_test, t_test) = load_mnist(flatten=True, normalize=False)
img = x_train[0]
label = t_train[0]
print(label)
print(img.shape)
img = img.reshape(28, 28)
print(img.shape)
img_show(img)
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
| Downloading train-images-idx3-ubyte.gz ...
Done
Downloading train-labels-idx1-ubyte.gz ...
Done
Downloading t10k-images-idx3-ubyte.gz ...
Done
Downloading t10k-labels-idx1-ubyte.gz ...
Done
Converting train-images-idx3-ubyte.gz to NumPy Array ...
Done
Converting train-labels-idx1-ubyte.gz to NumPy Array ...
Done
Converting t10k-images-idx3-ubyte.gz to NumPy Array ...
Done
Converting t10k-labels-idx1-ubyte.gz to NumPy Array ...
Done
Creating pickle file ...
Done!
5
(784,)
(28, 28)
|
神经网络处理
输入层:图像像素,共784个神经元
输出层:识别出来的数字,共10个神经元
隐藏层:设计为2层,第1层50个,第2层100个
代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
|
import sys, os
sys.path.append(os.pardir)
import numpy as np
import pickle
from source.dataset.mnist import load_mnist
from source.common.functions import sigmoid, softmax
def get_data():
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, flatten=True, one_hot_label=False)
return x_test, t_test
def init_network():
with open("./source/ch03/sample_weight.pkl", 'rb') as f:
network = pickle.load(f)
return network
def predict(network, x):
W1, W2, W3 = network['W1'], network['W2'], network['W3']
b1, b2, b3 = network['b1'], network['b2'], network['b3']
a1 = np.dot(x, W1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1, W2) + b2
z2 = sigmoid(a2)
a3 = np.dot(z2, W3) + b3
y = softmax(a3)
return y
|
init_network() 读入pickle文件中 已经学习好的权重参数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
x, t = get_data()
network = init_network()
accuracy_cnt = 0
for i in range(len(x)):
y = predict(network, x[i])
p= np.argmax(y)
if p == t[i]:
accuracy_cnt += 1
print("Accuracy:" + str(float(accuracy_cnt) / len(x)))
|
Accuracy:0.9352
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
x,_=get_data()
network=init_network()
W1,W2,W3=network['W1'],network['W2'],network['W3']
print(x.shape)
print(x[0].shape)
print(W1.shape)
print(W2.shape)
print(W3.shape)
|
(10000, 784)
(784,)
(784, 50)
(50, 100)
(100, 10)
单图片维数变化图
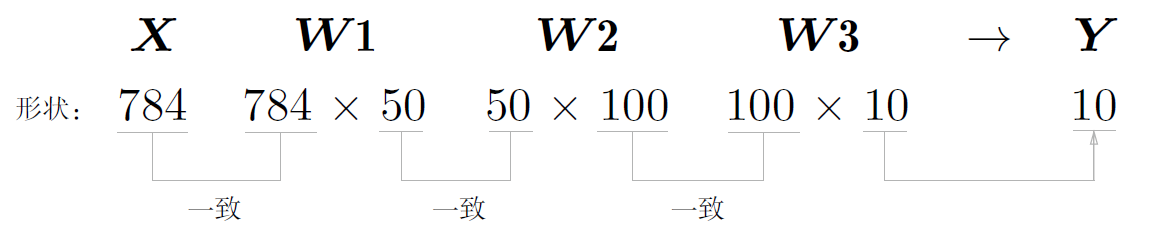
批处理
大多数数值计算的库都进行了能够高效处理代行数组运算的最优化。
使用批处理可以大幅缩短每张图像的处理时间
批处理代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
x, t = get_data()
network = init_network()
batch_size = 100
accuracy_cnt = 0
for i in range(0, len(x), batch_size):
x_batch = x[i:i+batch_size]
y_batch = predict(network, x_batch)
p = np.argmax(y_batch, axis=1)
accuracy_cnt += np.sum(p == t[i:i+batch_size])
print("Accuracy:" + str(float(accuracy_cnt) / len(x)))
|
Accuracy:0.9352
批处理维数变化:

总结
分类问题在输出层使用softmax函数,总和是1,每项输出代表该索引概率。
激活函数一般使用sigmoid函数或者ReLU函数,ReLU:Rectified Linear Unit,矫正线性单元
机器学习问题大体分为回归和分类问题
回归问题一般使用恒等函数
分类问题一般使用softmax函数
分类问题输出层设置为要分类的类别数
以批处理进行运算,可大幅提高运算速度。上面的结果中,未使用批处理是0.6s,而使用批处理是0.2s



